bdfgdfg
보완된(균형 잡힌)이진 탐색 트리의 이론 - 12장(1) 본문
이진 탐색 트리의 문제점과 AVL트리
이진 탐색 트리의 탐색 연산은 O(logN)의 시간 복잡도를 가진다.
트리의 높이를 하나씩 더해갈수록 추가할 수 있는 노드의 수가 두 배씩 증가하므로.
그런데 이전 장의 이진 탐색 트리는 문제점이 있는데 예로들어 10,20,30,40,50의 Key가 저장된 이진 탐색 트리를 보자.

이렇듯 노드가 한 쪽으로 쏠리게 된다. 만약 1부터 100까지의 Key값이 들어있는 노드들을 이진 탐색 트리에 넣을 시
내가 100이라는 값을 찾기 위해선 100번의 연산. 즉 O(N) 시간 복잡도를 가진다.
그렇다면 저장 순서를 바꾸면 어떨까?

똑같이 1 ~ 5까지의 Key값이 들어간 노드들이지만 위와 비교해서 제법 균형이 잡혀있고 트리의 높이도 줄어들었다.
이렇듯 앞서 구현한 이진 탐색 트리는 저장 순서에 따라 탐색의 성능에 큰 차이를 보인다.
이러한 이진 탐색 트리의 단점을 해결한 트리를 가리켜 '균형 잡힌 이진 트리'라 하며, 그 종류는 대략 다음과 같다.
1. AVL 트리
2. 2-3 트리
3. 2-3-4 트리
4. Red-Black 트리
5. B 트리
앞으로 구현할 균형 잡힌 이진 트리는 AVL트리.
AVL트리와 균형 인수
AVL 트리는 노드가 추가될 때, 그리고 삭제될 때 트리의 균형상태를 파악해 스스로 그 구조를 변경하여 균형을 잡는트리
AVL트리에서 균형의 정도를 표현하기 위해서 '균형 인수'라는 것을 사용하는데, 이 균형 인수는 다음과 같이 계산한다.
균형 인수 = 왼쪽 서브 트리의 높이 - 오른쪽 서브 트리의 높이
이제 각 노드별 균형 인수를 확인하는 예를 보자.

먼저 왼쪽 AVL트리에서 루트노드인 7을 기준으로 왼쪽 서브 트리의 높이는 3. 오른쪽 서브 트리의 높이는 1.
3 - 1 = 2. 그렇기에 루트 노드의 균형 인수는 2이다.
이렇듯. AVL 트리의 리밸런싱(균형을 잡기 위한 트리 구조의 재조정)시기는
균형 인수의 절댓값이 2 이상인 경우에 리밸런싱을 진행한다.
리밸런싱이 필요한 첫 번째 상태와 LL회전.

위의 경우. 5라는 노드가 왼쪽 서브 트리의 높이가 2. 오른쪽 서브 트리의 높이가 0.
2 - 0 = 2 이므로. 불균형 상태가 되었다.
즉 다음과 같이 간단하게 말할 수 있다.
"자식 노드 두 개가 왼쪽으로 연이어 연결되어서 균형 인수 +2가 연출되었다."
이렇게. 균형 인수가 무너진 노드를 기준으로 왼쪽 자식 노드가 2개인 경우.
Left Left 상태 -> LL상태 라고 표현한다.
그리고 이 LL상태에서 발생한 불균형의 해결을 위해 'LL회전'을 진행한다.
LL회전의 방법과 그 결과를 확인해보면 균형이 무너진 노드가 균형 인수가 +1인 노드의 오른쪽 자식 노드가 된다.
이것을 간단하게 코드로 생각해본다면

부모노드를 가리키는 포인터 변수 pNode와 자식노드를 가리키는 포인터 변수 cNode.
간단하게 앞서 구현한 메소드인 cNode->ChangeRightSubTree(pNode)를 전달하면 된다.
하지만 다음의 경우를 보자.

T1,T2,T3,T4는 높이가 동일한 서브 트리라고 가정한다.
그렇다면 이들은 5가 저장된 노드와 3이 저장된 노드의 균형 인수에 영향을 미치지 않는다.
(때문에 위의 상태도 LL상태)
T1,T2,T3,T4가 nullptr인 상태라면 앞서 보인 LL회전을 그대로 진행해도 괜찮다.
사실 T1,T2,T4는 LL상태라고 가정했을 때 신경쓸 요소는 아니다.
(왜냐하면 그대로 회전을 해도 트리는 유지가 되기에)
하지만 T3는 아니다. 3이 저장된 노드의 오른쪽 자식노드(T3)가 존재한다고하면.
그대로 5를 회전시켜 3의 오른쪽 자식 노드에 붙일 수 가없다.
하지만 균형 인수를 위해 5가 저장된 노드가 3이 저장된 노드의 오른쪽 자식노드에 붙여야하는데.
그렇다면 이 T3는 어디에 저장이 되어야 할까?
일반적으로 생각해보자. 원래 5의 왼쪽 자식 노드는 3이지만, LL회전을 통해 3의 오른쪽 자식 노드로 붙게된다면
5의 왼쪽 자식노드는 nullptr. 즉 빈상태가 될 것이다.
그렇다면 이곳에 T3를 붙이면 될 것이다.

이것은 이진 탐색 트리의 조건에도 부합한다.
앞서 구현한 cNode->ChangeRightSubTree(pNode)뿐만 아니라.
pNode->ChangeLeftSubTree(cNode->GetRightSubTree()) // nullptr이어도 상관없다! nullptr을 저장하게 될테니.
cNode->ChangeRightSubTree(pNode)
즉 먼저 균형 인수가 무너진 부모노드의 왼쪽 자식을 자식노드의 오른쪽 서브 트리의 주소로 바꾼 뒤,
LL회전을 진행하는 것.
리밸런싱이 필요한 두 번째 상태와 RR회전
앞서 LL상태가 균형인수가 2인 불균형 노드가 왼쪽 자식 노드가 연달아 있는 상태였다면,
RR상태는 오른쪽 자식 노드가 연달아 있는 상태.
그렇기에 RR회전은 RR상태의 균형을 잡기 위한 회전을 의미한다.
LL상태와 RR상태의 유일한 차이는 방향이다.

불균형 노드 5가 회전되어 안착되는 자리는 자식 노드(7)의 왼쪽 자식 노드이다.
물론 이것도 LL상태와 마찬가지로 T1,T2,T4는 신경을 꺼도 좋지만
T3의 경우는 예외이다.
이것도 마찬가지로

회전을 하게 된다면 이런 형태.
왜? 상식적으로 5의 오른쪽 자식 노드인 7을 대상으로 회전을 하여 7의 왼쪽 자식노드에 안착했으니.
5의 오른쪽 자식노드는 빈공간이 된다.
이것을 코드로 표현해본다면
pNode->ChangeRightSubTree(cNode->GetLeftSubTree()) // nullptr이어도 상관없다! nullptr을 저장하게 될테니.
cNode->ChangeLeftSubTree(pNode)
리밸런싱이 필요한 세 번째 상태와 LR회전
이제 어느정도 감이 잡혔다.
LR회전은 LR상태에서의 리밸런싱을 위한 회전방법.
그렇다면 LR상태란 자식 노드가 왼쪽으로 하나, 그리고 이어서 오른쪽으로 하나 달린 상태를 뜻한다.

이것도 일반화를 해본다면

LR상태에서 LR회전은 어떻게 해야할까?
LR상태는 앞서 보인 LL상태,RR상태 보다는 좀 더 복잡하다. 그 이유는 한번의 회전으로는 균형을 잡을 수가 없기때문.
따라서 다음과 같은 방법을 취한다.
"LR상태를 한 번의 회전으로 균형이 잡히는 LL상태나 RR상태로 일단 바꾼다."
LL상태나 RR상태로 바꾼다면 이후의 리밸런싱 과정은 매우 간단하다.
그렇다면 어떻게 LL상태나 RR상태로 바꿀 수 있을까?
바로 LR상태는 RR회전을 통해서 LL상태가 되게 할 수 있다.
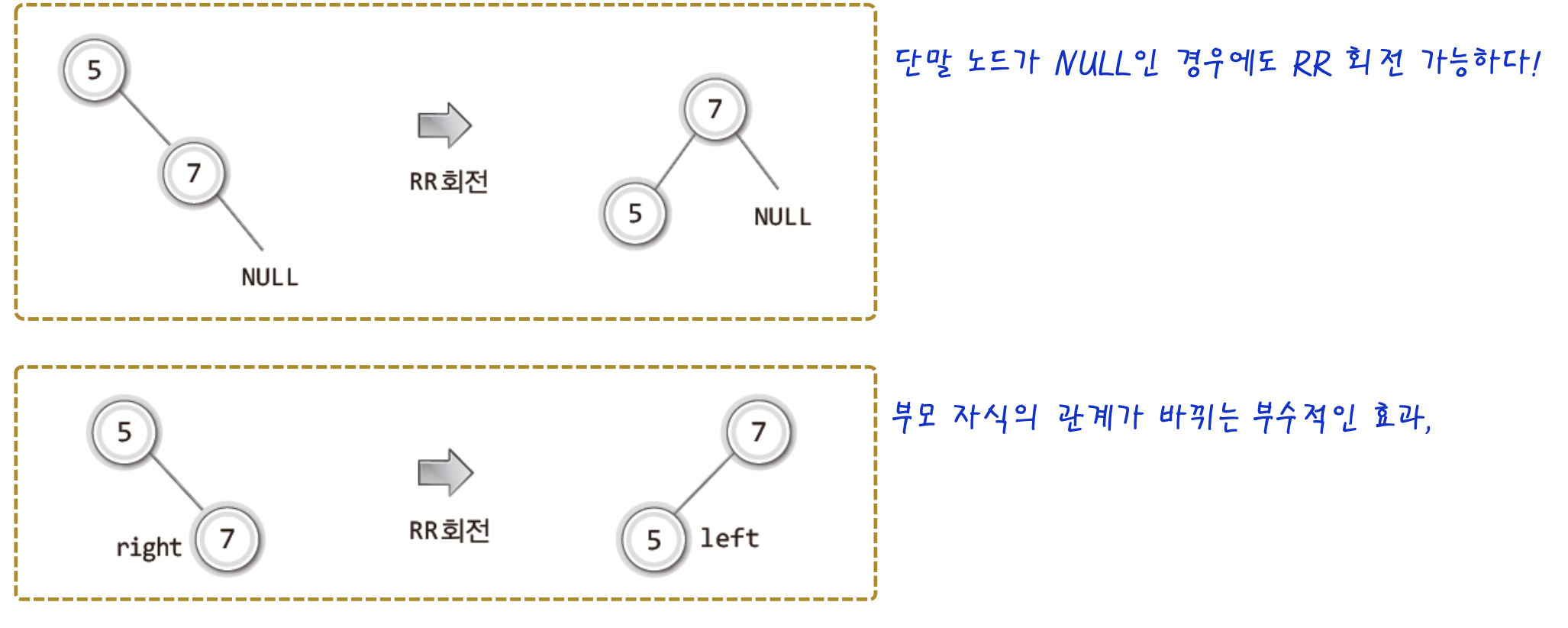
RR회전이나 LL회전은 각각 RR상태 LL상태를 위한 리밸런싱 방법이다.
다만, 그 방법이 무조건 그 순간에만 사용가능하다는 것은 아니다.(물론 위 그림의 형태는 리밸런싱과는 거리가있음)
어쨌든 중요한 것은 위 그림과 같이 RR회전을 통해 5와 7이 저장된 노드의 관계를 바꿀 수 있다는 것.
그럼 이제 다시 돌아와 RR회전을 하여 LL상태로 만들어 보자.

보면 알겠지만 LR상태를 RR회전을 통해 LL상태로 바꾸고 있다.
(1이 저장된 노드가 3의 왼쪽 자식 노드로 회전)
이제 이 LL상태에서 LL회전을 시킨다면 트리의 균형이 잡히는 일이다.

이런식으로.
참고로 LR상태의 일반화에서.

T1,T2,T3,T4를 고민하지 않아도 될까? 그 부분은 고민하지 않아도 된다.
왜? 우선 LR상태는 LL상태로 만들기 위해 RR회전을 하고 LL상태가 되었을 때 LL회전을 적용한다.
이 과정에서 RR회전과 LL회전이 사용이 된다.
즉 RR회전이 위에서 설명할 때 T3를 유지하기 위해서 먼저 균형이 무너진 노드에 오른쪽 자식노드를
오른쪽 자식노드의 왼쪽 자식 노드를 오른쪽 자식 노드로 붙인 다음 회전을 하였다.
위 그림을 토대로 설명하면,

이렇게 앞서 구현한 LL회전과 RR회전이 T3의 경우를 체크하므로 LR상태에서는 T1,T2,T3,T4의 경우는 생각하지 않아도 된다.
리밸런싱이 필요한 네 번째 상태와 RL회전
RL상태를 해결하기 위한 RL회전.
LR회전이 부분 RR회전을 한 뒤 LL상태가 되면 LL회전을 진행.
RL회전은? 부분 LL회전을 한 뒤 RR상태가 되면 RR회전을 진행할 것이라고 예상이 가능하다.

RL상태도 간단하다.
LR상태가 왼쪽으로 자식하나 이녀석의 오른쪽 자식 하나.
RL상태는 오른쪽으로 자식하나 이녀석의 왼쪽 자식 하나. 인 상태가 RL상태.
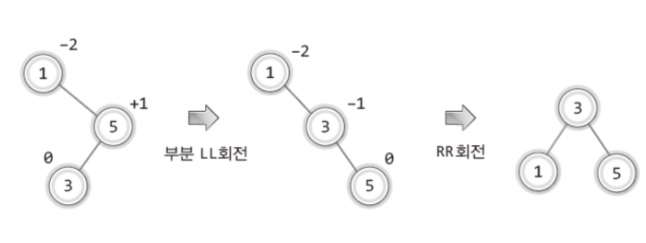
앞서 말했듯 이녀석도 LR상태의 반대라고 생각하면 된다.
그리고 부분 LL회전과 RR회전함에 있어서 T1,T2,T3,T4의 요소는 고려하지 않아도 된다.
간단정리
1. LL상태 - LL회전
2. RR상태 - RR회전
3. LR상태 - 부분 RR회전 후 LL상태로 만든 다음 LL회전.
4. RL상태 - 부분 LL회전 후 RR상태로 만든 다음 RR회전.
