bdfgdfg
최소 비용 신장 트리와 크루스칼 알고리즘 - 14장 (3) 본문
최소 비용 신장 트리
트리는 그래프의 한 유형.
다음 그래프를 보고 정점 B에서 정점 D에 이르는 모든 경로를 찾아서 열거해본다.

이렇게 두 개의 정점을 잇는 간선을 순서대로 나열한 것을 가리켜 '경로'라 한다.
그리고 위의 네 경로와 같이 동일한 간선을 중복하여 포함하지 않는 경로를 가리켜 '단순 경로'라 한다.
단순 경로가 아닌 예를 들어보면
B-A-C-B-A-D -> B와 A를 잇는 간선이 두 번 포함됨.
그렇다면 A-B-C-A는 단순 경로가 일까?
단순 경로가 맞다. A정점이 두 번 등장하지만 중복된 간선이 포함되지 않기 때문이다.
이렇게 단순 경로이면서 시작과 끝이 같은 경로를 가리켜 '사이클'이라 한다.

간단히 말해 사이클은 어느 정점에서 다른 경로를 통해 다시 돌아올 수 있다면 사이클이라 한다.
그리고 이번에 공부할 최소 비용 신장 트리는 이 사이클을 형성하지 않는 그래프이다.
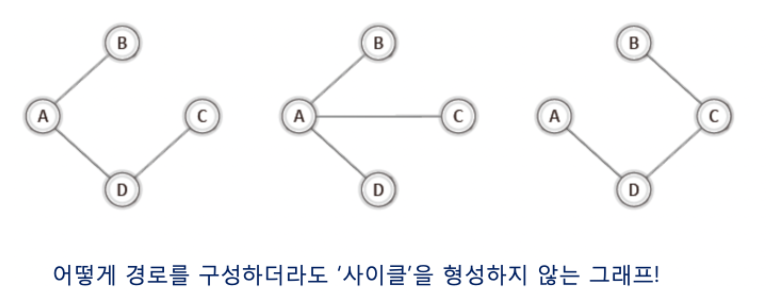
그리고 이 그림을 90~180정도 회전시켜보면 트리와 같은 그림이 나타나므로 위 그림과 같이 사이클을 형성하지 않는
그래프들을 가리켜 '신장 트리'라 한다.
최소 비용 신장 트리의 이해와 적용
사이클을 형성하지 않는 신장 트리의 특징을 다시 정리해본다
1. 그래프의 모든 정점이 간선에 의해 하나로 연결되어 있다.
2. 그래프 내에서 사이클을 형성하지 않는다.
3. 그리고 위에서 설명하진 않았지만 최소 비용 신장 트리의 특징으로 정점의 수 - 1 = 간선의 수가 된다.
이제 가중치 그래프를 대상으로 신장 트리를 구성할 수 있다.

그리고 위와 같은 그림에서 '신장 트리'의 모든 간선의 가중치 합이 최소인 그래프를 가리켜 '최소 비용 신장 트리'라 함.

사이클을 형성하지 않고, 모든 정점과 하나씩 연결되어 있으며 모든 간선의 합이 최소인 그래프.(최소 비용 신장 트리)
또 다른 예를 들어보면

위와 같이 지역간의 거리를 가중치로 들고 있는 그래프에서 최소 비용 신장 트리를 구하면 위와 같은 그래프가 만들어진다.
최소 비용 신장 트리의 구성을 위한 알고리즘
최소 비용 신장 트리의 구성에 사용되는 대표적인 알고리즘 두 가지가 있다.
1. 크루스칼(Kruskal) 알고리즘
- 가중치를 기준으로 간선을 정렬한 후에 MST(최소 비용 신장 트리)가 될 때까지 간선을 하나씩 선택 또는 삭제해나가는 방식.
2. 프림(Prim) 알고리즘
- 하나의 정점을 시작으로 MST가 될 때까지 트리를 확장해 나가는 방식
여기서는 크루스칼 알고리즘을 통해 MST를 구현한다.
이제 크루스칼 알고리즘의 예를 본다.
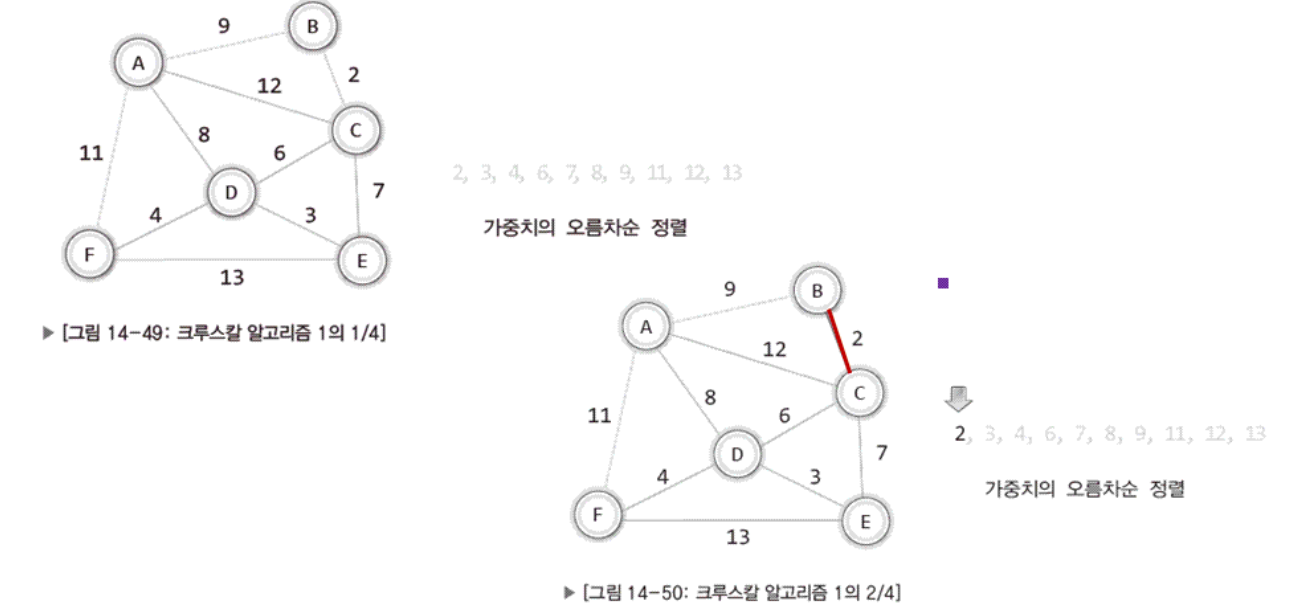
이렇게. 무방향 가중치 그래프가 하나가 있다고 가정한다.
그리고 우리는 '최소' 비용 신장 트리를 구하니 모든 간선의 가중치를 오름차순으로 정렬한다.
그리고 여기서 이제 가중치가 낮은 간선부터 하나씩 추가하면서 선택할지 아니면 지나갈지를 결정한다.
(마냥 낮은 간선을 무작정 선택할 수는 없다 -> 사이클을 형성하지 않기 위해)
1. 우선 첫번째로 가장 낮은 가중치를 가지는 간선 2를 선택.

2. 그 다음 3,4,6을 차례로 간선을 선택하면서 사이클을 형성하지 않는지. 확인하면서 선택한다.
3. 이제 7이라는 간선을 선택할 차례. 근데 위 그림만 보아도 바로 사이클이 형성된다는 것을 알 수 있다.
4. 그렇기에 바로 다음 8이라는 간선을 선택할 차례.

5. 간선 8을 연결하고 보면 그림에선 최소 비용 신장 트리가 완료되었다는 것을 알 수 있다.
6. 이것을 코드상에서는 앞서 말했듯이. 신장 트리의 조건은 정점 - 1 = 간선의 수.라고 하였다. 즉 6 - 1 = 5가 만족했으므로 최소 비용 신장 트리가 완성.
크루스 칼 알고리즘의 흐름을 다시 정리해보면
1. 가중치를 기준으로 간선을 오름차순으로 정렬한다. (내림차순으로 반대로 가중치가 높은 간선을 빼는 방식도 존재)
2. 낮은 가중치의 간선부터 시작해서 하나씩 그래프에 추가
3. 사이클을 형성하는 간선은 추가 X
4. 간선의 수가 정점의 수보다 하나 적을 때 MST(최소 비용 신장 트리)의 완성.
크루스 칼 알고리즘의 구현 모델
구현 모델은 가중치를 기준으로 간선을 내림차순으로 정렬한 다음 높은 가중치의 간선을 하나씩 그래프에서 제거한다.
앞서 구현한 DFS모델에서 조금 더 추가한 방식의 크루스칼 모델을 만든다.
DFS를 사용하는 이유는 높은 가중치의 간선을 제거한 후에도 이 간선에 의해 연결된 두 정점을 연결하는 경로가
있는지 체크하기 위함.
그리고 가중치를 기준으로 간선을 정렬해야 하기에 우선순위 큐도 포함하여 활용한다.
#pragma once
class LinkedList;
#include "Heap.h"
class ALGraphKruskal
{
public:
ALGraphKruskal() = delete;
ALGraphKruskal(int inputV); // 내부 달라짐.
~ALGraphKruskal(); // 이전과 동일
void AddEdge(int fromV, int toV, int weight); // 가중치 값 매개변수 추가.
void ShowGraphEdgeInfo(); // 이전과 동일
bool VisitVertex(int visitV); // 이전과 동일
void DFShowGraphVertex(int startV); // 이전과 동일
void ConkruskalMST(); // 추가. 최소 비용 신장 트리의 구성
void ShowGraphEdgeWeightInfo(); // 추가. 가중치 정보 출력
void RemoveEdge(int fromV, int toV); // 추가. 간선의 소멸 (무방향그래프이니 RemoveWayEdge를 두번호출)
void RemoveWayEdge(int fromV, int toV); // 추가. 한쪽 방향의 간선 소멸
void RecoverEdge(int fromV, int toV, int weight); // 추가. 간선 다시붙이기.
bool IsConnVertex(int v1, int v2); // 인자로 전달된 두 정점이 연결되어 있다면 true 아니면 false
private:
int numV;
int numE;
int* visitInfo;
LinkedList* adjList;
Heap priorityQueue; // 우선순위 정보.
};먼저 함수 하나하나를 따져본다. (동일한 것들은 제외) - ALGraphKruskal
1. 생성자와 우선순위 큐에 넣을 함수
int PQWeightComp(Edge d1, Edge d2) // 우선순위 큐 함수포인터에 등록하기 위한 함수.
{
// 첫번째 인자로 전달된 간선의 가중치가 크면 양수 반환
// 두번째 인자로 전달된 간선의 가중치가 크면 음수 반환
return d1.weight - d2.weight;
}
ALGraphKruskal::ALGraphKruskal(int inputV) : numV(inputV), numE(0), priorityQueue(PQWeightComp)//등록
{
adjList = new LinkedList[numV]();
visitInfo = new int[numV];
memset(visitInfo, 0, sizeof(int) * numV); // 0으로 초기화.
}
ALGraphKruskal::~ALGraphKruskal()
{
delete[] adjList;
delete[] visitInfo;
}2. AddEdge
void ALGraphKruskal::AddEdge(int fromV, int toV, int weight)
{
Edge edge = { fromV, toV,weight }; // 구조체 초기화.
adjList[fromV].push_front(toV);
adjList[toV].push_front(fromV);
++numE;
priorityQueue.Insert(edge);
}기존의 DFS, BFS헤더 파일의 AddEdge 메서드에서 매개변수 weight(가중치)값을 하나 더 받는다.
그리고 Edge변수를 우선순위 큐에 넣어준다. (위 함수에 따라 가중치가 높은 녀석이 우선순위가 높다)
3. ConKruskalMST - 핵심 메소드 MST를 만든다.
void ALGraphKruskal::ConkruskalMST()
{
Edge recvEdge[20]; // 복원할 간선의 정보 저장.
Edge edge;
int eidx = 0;
int i;
// MST를 형성할 때까지 아래의 while문 반복
while (numE + 1 > numV) // MST 간선의 수 + 1 == 정점의 수
{
// 우선순위 큐에서 가중치가 제일 높은 녀석을 뺸다.
edge = priorityQueue.Delete();
// 우선순위 큐에서 꺼낸 간선을 그래프에서 제거한다.
RemoveEdge(edge.v1, edge.v2); // 밑에서 함수 소개
// 간선을 삭제하고 나서도 두 정점을 연결하는 경로가 있는지 확인
if(!IsConnVertex(edge.v1,edge.v2)) // 밑에서 함수 소개
{
// 경로가 없다면 삭제한 간선을 복원한다.
RecoverEdge(edge.v1,edge.v2,edge.weight); // 밑에서 함수 소개
// 복원한 간선의 정보를 별도로 저장.
recvEdge[eidx++] = edge;
}
}
for (i = 0; i < eidx; ++i) // 회복된 녀석들 위에서 없앴으니 우선순위 큐에 다시넣어야함.
priorityQueue.Insert(recvEdge[i]);
}복원할 간선의 정보(Edge)를 담는 이유는 (배열)
위 함수는 무조건 일단 내림차순으로 된 간선들을 제거한다. 그리고 제거했는데 그 정점을 다시 찾을 수 없다면
다시 연결해주고 우선순위 큐에서 없앴던 정보를 다시 넣어주기 위함.
예로 들어
while문에서 A와 B정점 간의 가중치 값을 받아오고 (우선순위 큐에서 나왔다)
그 두 경로를 없앤다. 그리고 if문을 통해 IsConnVertex(밑에서 소개함) 함수를 통해 두 정점을 DFS를 통해 찾을 수 있는지 확인하고 못 찾는다면 다시 연결.
-> 여기서 우선순위 큐는 날려버렸으니 다시 복원을 위해 우선순위 큐에 넣는 모습 (밑에 반복문)
4. ConKruskalMST 메서드에서 사용된 RemoveEdge, IsConnVertex, RecoverEdge 메서드.
1. RemoveEdge - 그래프에서 간선을 삭제.
2. IsConnVertex - 두 정점이 연결되어 있는지 확인
3. RecoverEdge - 삭제된 간선을 다시 삽입.
먼저 RemoveEdge
void ALGraphKruskal::RemoveEdge(int fromV, int toV)
{
RemoveWayEdge(fromV, toV);
RemoveWayEdge(toV, fromV);
--numE;
}책에서 무방향 그래프를 구현했으므로 간선 두 개를 없애야 함.
그다음 RemoveWayEdge.
void ALGraphKruskal::RemoveWayEdge(int fromV, int toV)
{
int edge;
if (adjList[fromV].LFirst())
{
edge = adjList[fromV].iterator()->GetData();
if (edge == toV)
{
adjList[fromV].pop_cur();
return;
}
while (adjList[fromV].LNext())
{
edge = adjList[fromV].iterator()->GetData();
if (edge == toV)
{
adjList[fromV].pop_cur();
return;
}
}
}
}인접 리스트로 구현된 무방향 가중치 그래프에서 각 fromV에 해당하는 링크드 리스트 인덱스에 접근해
toV가 존재하는지 찾는다.
있다면 노드를 제거 없다면 그냥 종료.
그 다음 RecoverEdge
void ALGraphKruskal::RecoverEdge(int fromV, int toV, int weight)
{
adjList[fromV].push_front(toV);
adjList[toV].push_front(fromV);
++numE;
}두 간선(무방향)의 경로를 다시 연결.
5. IsConnVertex 메서드. 정점을 없애고 난 후 두 정점 간의 연결고리가 존재하는지 확인.
가중치가 높은 간선을 없앤다고 끝이 아니라.
신장 트리의 조건.
그래프의 모든 정점이 간선에 의해 하나로 연결되어 있어야 하므로.
DFS로 정점을 찾지 못한다면 다시 연결해야 한다.
bool ALGraphKruskal::IsConnVertex(int v1, int v2)
{
Stack<int> s;
int visitCount = 0;
int visitV = v1;
int nextV;
VisitVertex(visitV);
s.Push(visitV);
++visitCount;
while (adjList[visitV].LFirst())
{
nextV = adjList[visitV].iterator()->GetData();
bool visitFlag = false;
// 정점을 찾다가 목표를 찾는다면 true
if (nextV == v2)
{
// 함수가 반환하기전 초기화를 진행.
memset(visitInfo, 0, sizeof(int) * numV);
return true;
}
// 목표가 아니라면 또다시 방문하는것을 막기위해.
if (VisitVertex(nextV))
{
visitV = nextV;
s.Push(visitV);
visitFlag = true;
++visitCount;
}
else
{
while (adjList[visitV].LNext())
{
nextV = adjList[visitV].iterator()->GetData();
if (nextV == v2)
{
// 함수가 반환하기전 초기화를 진행.
memset(visitInfo, 0, sizeof(int) * numV);
return true;
}
if (VisitVertex(nextV))
{
visitV = nextV;
s.Push(visitV);
visitFlag = true;
++visitCount;
break;
}
}
}
if (visitFlag == false)
{
if (s.Empty())
break;
else
{
s.Pop();
visitV = s.GetTop();
if (s.Empty() && visitCount == numV)
{
memset(visitInfo, 0, sizeof(int) * numV);
return false; // 못찾음.
}
}
}
}
memset(visitInfo, 0, sizeof(int) * numV);
return false; // 못찾음.
}기존의 DFS함수 내용을 거의 그대로 들고 왔다.
차이는 링크드 리스트 배열 visitV 인덱스에 저장된 노드를 대상으로 DFS를 진행하면서 nextV가 v2(찾고자 하는 정점)이 있는지를 찾는 것이다.
true를 반환하면 연결고리가 있으므로 간선을 삭제해도 된다는 것이고, false를 반환한다면 다시 연결해줘야 한다는 것.
추가로 이제 우선순위 큐에 남은 가중치의 정보를 토대로 연결된 간선과 가중치 값을 확인하는 메서드.
-> ShowGraphEdgeWeightInfo()
void ALGraphKruskal::ShowGraphEdgeWeightInfo()
{
Heap copyPQ(priorityQueue); // 복사생성자를 깊은 복사로 만듬
Edge edge;
std::cout << std::endl;
while (!copyPQ.IsEmpty())
{
edge = copyPQ.Delete();
std::cout << static_cast<char>(edge.v1 + 'A') << " - " << static_cast<char>(edge.v2 + 'A') << ", WEIGHT : " << edge.weight << std::endl;
}
}하나씩 뽑아오면서 확인한다.
main.cpp와 결과.
enum // 정점이름 상수화.
{
A = 0, B, C, D, E, F, G, H, I, J
};
int main()
{
ALGraphKruskal a(6);
a.AddEdge(A, B, 9);
a.AddEdge(B, C, 2);
a.AddEdge(A, C, 12);
a.AddEdge(A, D, 8);
a.AddEdge(D, C, 6);
a.AddEdge(A, F, 11);
a.AddEdge(F, D, 4);
a.AddEdge(D, E, 3);
a.AddEdge(E, C, 7);
a.AddEdge(F, E, 13);
a.ConkruskalMST();
a.ShowGraphEdgeInfo();
a.ShowGraphEdgeWeightInfo();
cout << endl;
return 0;
}
'CS > 자료구조 알고리즘' 카테고리의 다른 글
| 프림(Prim) MST 알고리즘 (0) | 2021.08.01 |
|---|---|
| Disjoint Set - Union Find (0) | 2021.07.30 |
| 깊이 우선 탐색(DFS)와 너비 우선 탐색(BFS) - 14장 (2) (0) | 2021.07.12 |
| 그래프(Graph)의 이해와 종류 - 14장 (1) (0) | 2021.07.11 |
| 해시 테이블, 충돌 문제의 해결책 - 13장(2) (0) | 2021.07.11 |



