변환(Transform) - Graphics

변환(Transform)

그래픽스에서 물체의 변환을 위해 행렬을 사용한다.

Scale(신축),Rotation(회전),Translation(이동)의 변환행렬부터 살펴본다.

 -> 위를 SRT변환 행렬이라 하며 로컬공간에서 위의 행렬들을 곱하여 월드공간에 올린다.(단위 행렬이어도 상관없다)

 -> 로컬공간은 물체 중심의 자신만의 좌표 공간.

 -> 월드공간은 하나의 월드(게임 세상)가 기준이되는 좌표 공간.

 -> 왼손 좌표계를 사용하는 DirectX에서는 S * R * T * M(기타 행렬)의 순서로 최종 변환 행렬을 결합해야 한다.

 

Scale행렬

스케일 행렬은 월드 공간에 올라갈 물체의 크기를 바꾼다.

출처 - http://egloos.zum.com/EireneHue/v/982704

물체의 크기를 바꾸기 위한 행렬을 곱할 떄는 위의 Scale행렬을 곱하게 되는데, 주 대각선상에서 물체의 3차원 좌표가 그대로 곱해지는것을 알 수 있다.

DirectX에서는 왼손 좌표계를 사용하여 1 x 3의 행벡터를 이용한다.

하지만 위의 행렬의 크기를 보면 3x3크기가 아닌 4x4의 크기를 사용하게 되는데, 그 이유는 S * R * T * M의 연산을 매번 정점마다 정점하나 * S, 정점하나 * R 하지않고 행렬의 결합법칙을 이용하여 한번의 행렬과의 곱연산으로 처리하기 위해

동차 좌표계를 이용한 것.

 -> 동차 좌표계란 한 차원의 좌표(N차원)에서 하나의 좌표(N + 1)를 추가로 표현한 것.

 -> 즉 정점의 위치를 나타내는 x,y,z의 1 * 3 행 벡터에서 w성분을 추가한 x,y,z,w의 1 * 4 행 벡터로 표현. (행렬 내항일치)

 -> 위의 w성분에서는 0을 넣을 시 방향을 의미하고 그렇지 않으면 위치를 의미한다. (w가 1)

 -> 신축과 회전만을 고려한다면 3 x 3행렬만으로도 가능하지만 이동변환까지 한번의 행렬과의 곱연산으로 처리하기 위함. 더 자세한건 이동행렬에서

 

좀 더 이해하기 쉽게 그림으로 보자.

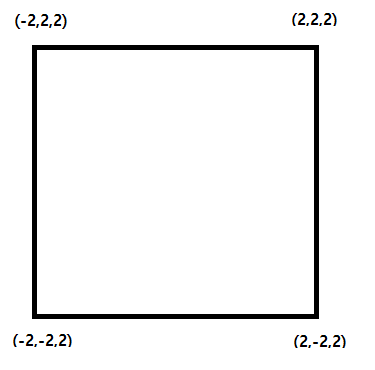
위와 같이 한 사각형 면을 가지는 물체가 존재하고 각 정점의 좌표가 위와같다고 보자.

저 사각형면의 크기를 정확히 3배로 키우고 싶을 떄 밑과같이 행렬의 연산을 통해 크기를 키울 수 있다.

 -> 동차좌표계를 이용

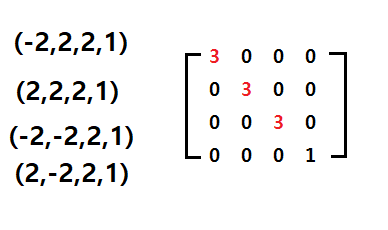
그럼 각 정점의 값은 각각

(-6,6,6,1)

(6,6,6,1)

(-6,-6,6,1)

(6,-6,6,1)

모든 정점의 좌표의 x,y,z성분이 정확히 3배씩 증가한것을 알 수 있다.

 

간단하게 테스트 하기 위해 Dx환경에서의 2차원 공간에서의 크기 변환을 본다.

Matrix2x2 S; // 2x2크기의 행렬. 
// 주 대각선
S._11 = 2.0f;
S._12 = 0.0f;
S._21 = 0.0f;
S._22 = 2.0f;

// NDC좌표로 변환된 각 정점의 좌표들
Vector2 v0 = m_rectObj->m_vertexList[0].vertexCoord * S;
Vector2 v1 = m_rectObj->m_vertexList[1].vertexCoord * S;
Vector2 v2 = m_rectObj->m_vertexList[2].vertexCoord * S;
Vector2 v3 = m_rectObj->m_vertexList[3].vertexCoord * S;

m_rectObj->m_vertexList[0].vertexCoord = v0;
m_rectObj->m_vertexList[1].vertexCoord = v1;
m_rectObj->m_vertexList[2].vertexCoord = v2;
m_rectObj->m_vertexList[3].vertexCoord = v3;

SRT변환은 월드행렬에 들어가게 되고, DX에서는 정점쉐이더 단계에서 처리되지만, 위에서는 모두 처리되고 난 후의 좌표에서 처리.

 

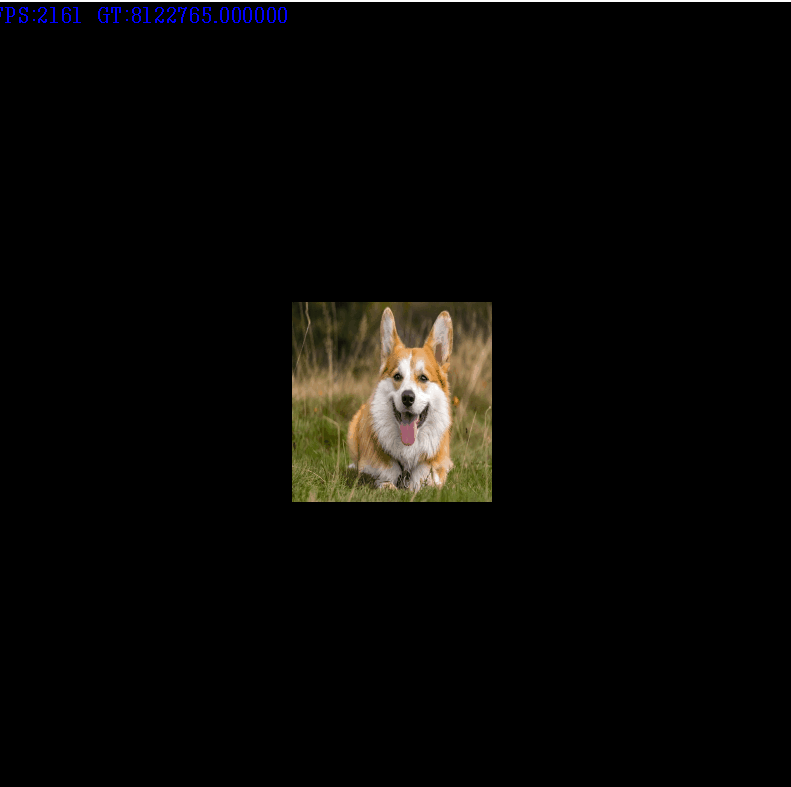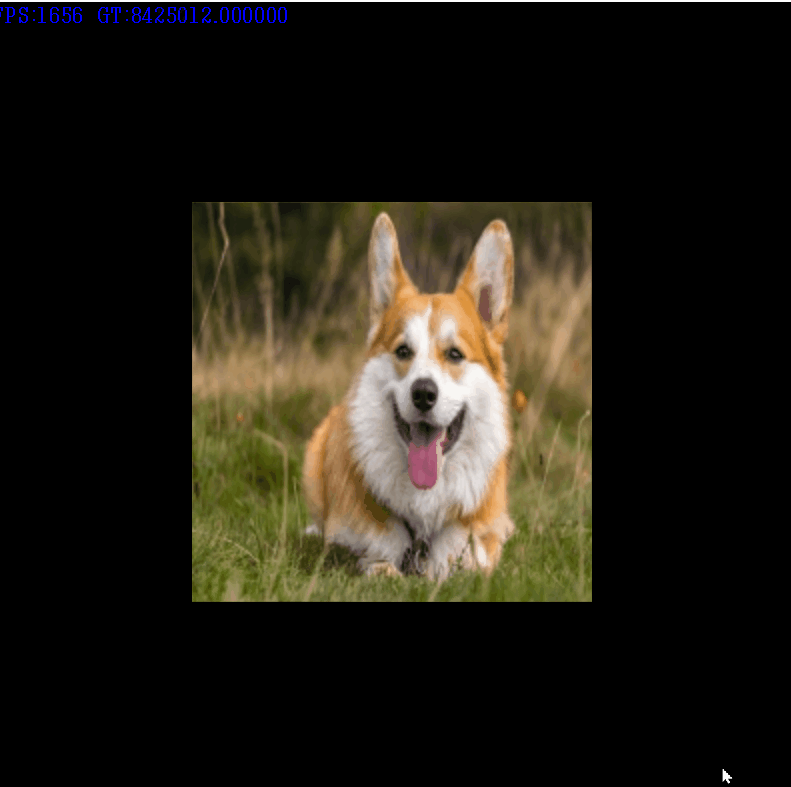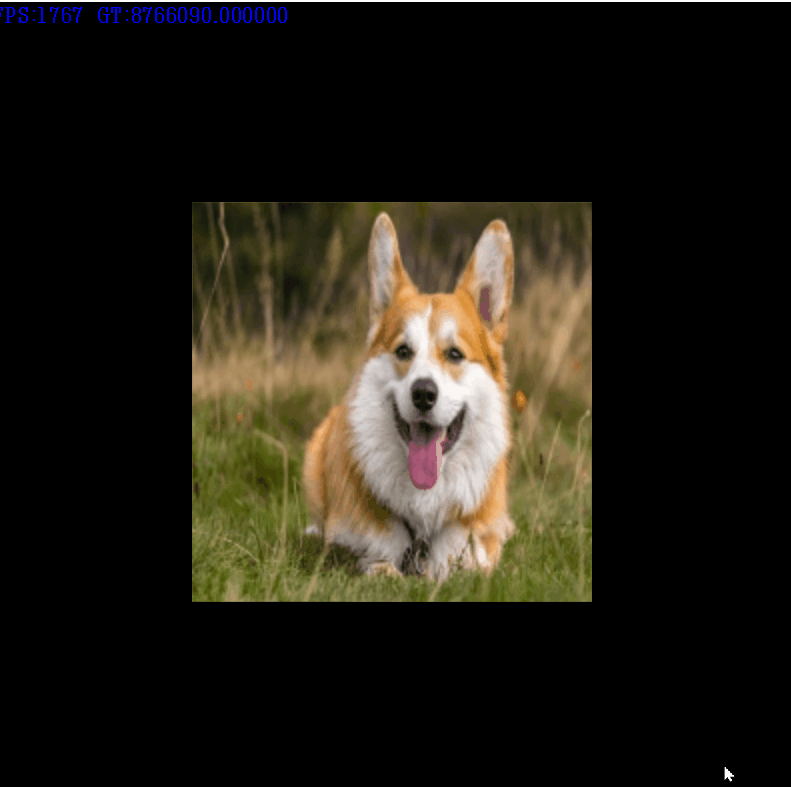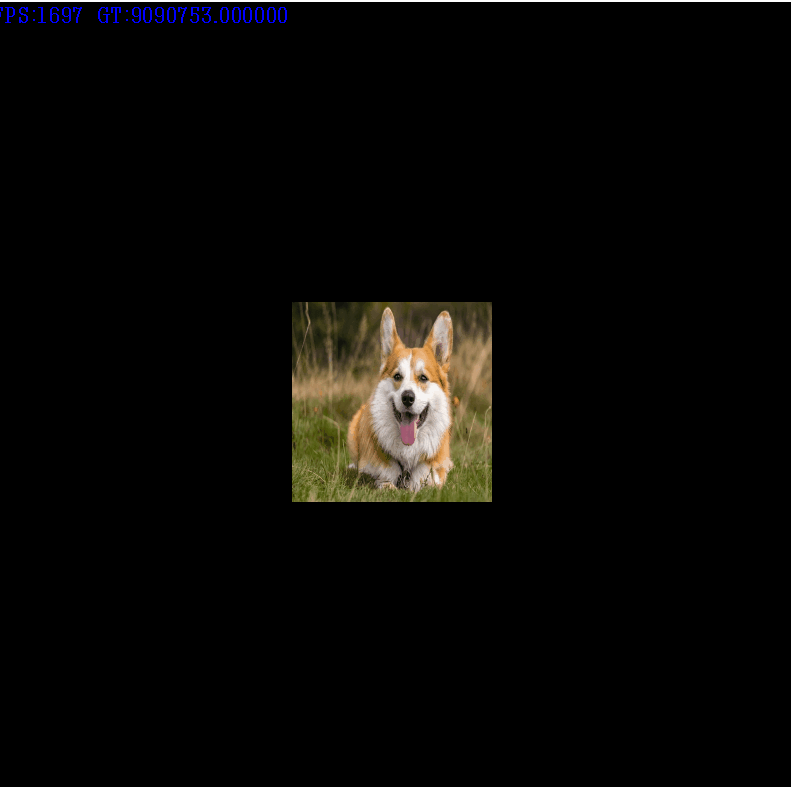
위 처럼 적용이 잘되는것을 알 수 있다.

 

Rotation행렬

Rotation 행렬은 월드 공간에 올라갈 물체를 회전시킨다.

각 축의 회전행렬을 보면 x축에 해당하는 1열,y축에 해당하는 2열, z축에 해당하는 3열에 각각 변화가 존재하지 않는다.

즉 회전하고자 하는 축의 원소는 변경하지 않고 유지되며 나머지 2개의 축 원소들만 회전되는 것.

 

회전행렬 또한 4x4크기의 행렬. 정점의 좌표애서 w성분을 추가하여 각 축에 해당하는 회전행렬을 곱하면

왼손 좌표계를 사용하는 DirectX에서는 X축 회전은 반시계 방향회전, Y축회전은 시계방향 회전, Z축 회전은 반시계 방향 회전이 된다.

 

회전행렬 또한 간단하게 테스트해본다.

Matrix2x2 R;
R._11 = cos(DegreeToRadian((20))); //0
R._12 = sin(DegreeToRadian((20)));
R._21 = -sin(DegreeToRadian(20));
R._22 = cos(DegreeToRadian(20));

// NDC좌표로 변환된 각 정점의 좌표들
Vector2 v0 = m_rectObj->m_vertexList[0].vertexCoord * R;
Vector2 v1 = m_rectObj->m_vertexList[1].vertexCoord * R;
Vector2 v2 = m_rectObj->m_vertexList[2].vertexCoord * R;
Vector2 v3 = m_rectObj->m_vertexList[3].vertexCoord * R;

m_rectObj->m_vertexList[0].vertexCoord = v0;
m_rectObj->m_vertexList[1].vertexCoord = v1;
m_rectObj->m_vertexList[2].vertexCoord = v2;
m_rectObj->m_vertexList[3].vertexCoord = v3;

cos,sin함수는 C++의 cmath헤더를 추가하여 사용하였고, 인자로 라디안값을 받으니 degree값을 radian으로 변환해주어야 한다.

 -> DegreeToRadian = Degree * (PI / 180)

 -> RadianToDegree = Radian * (180 / PI)

 

 

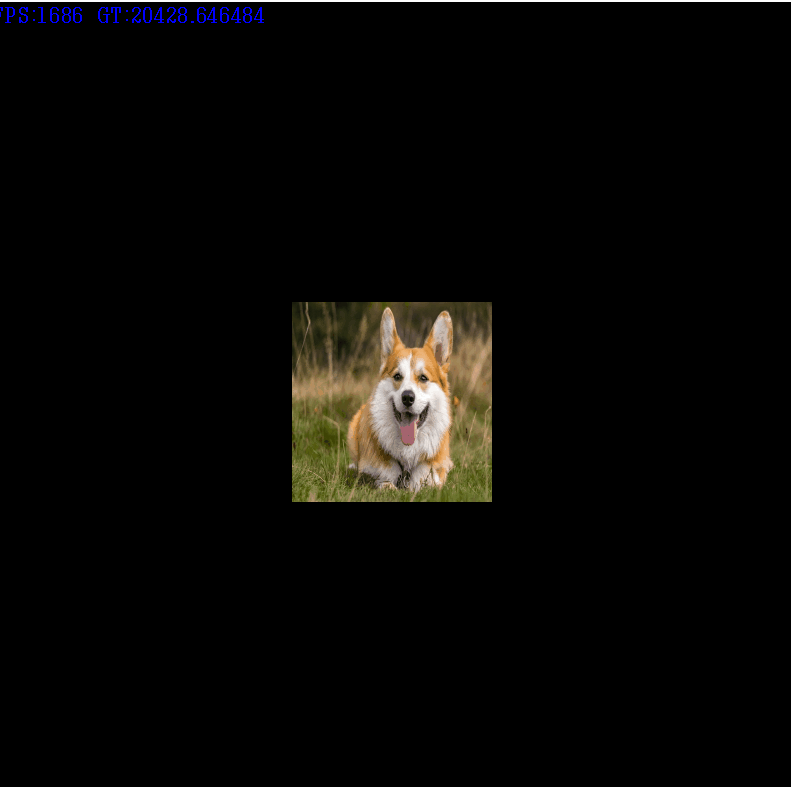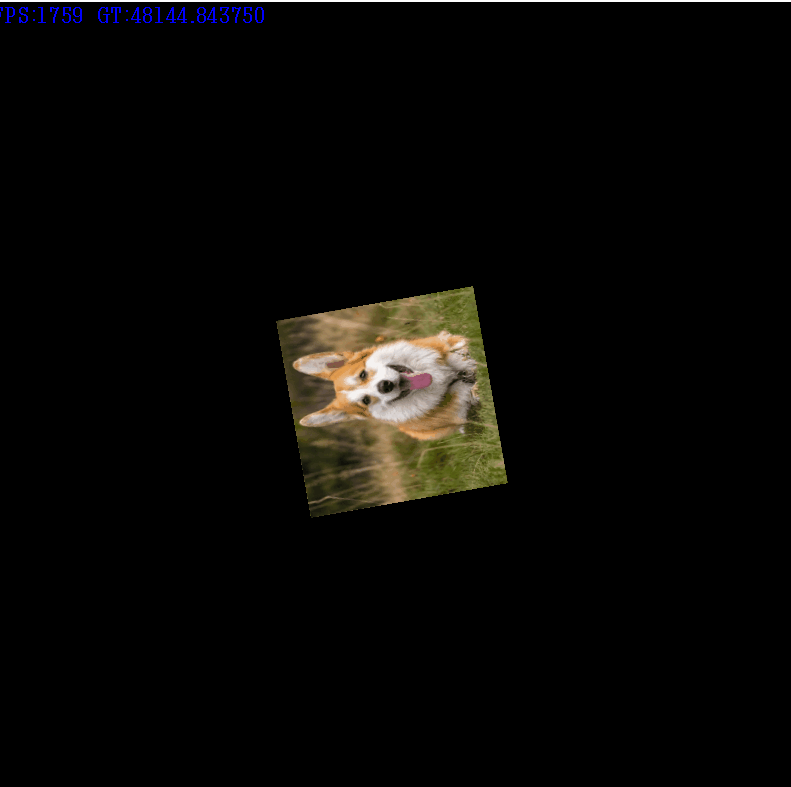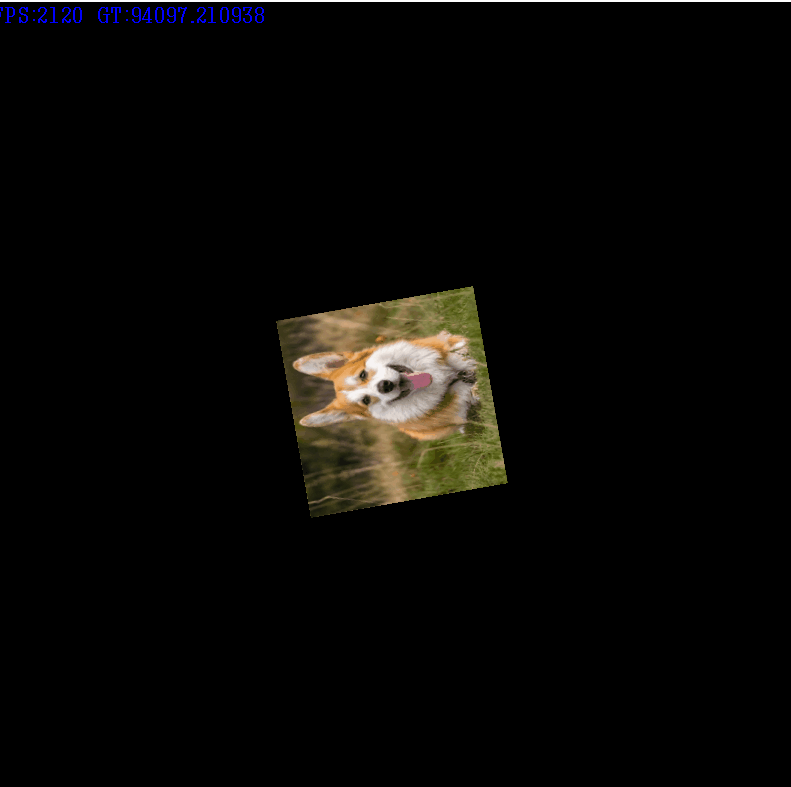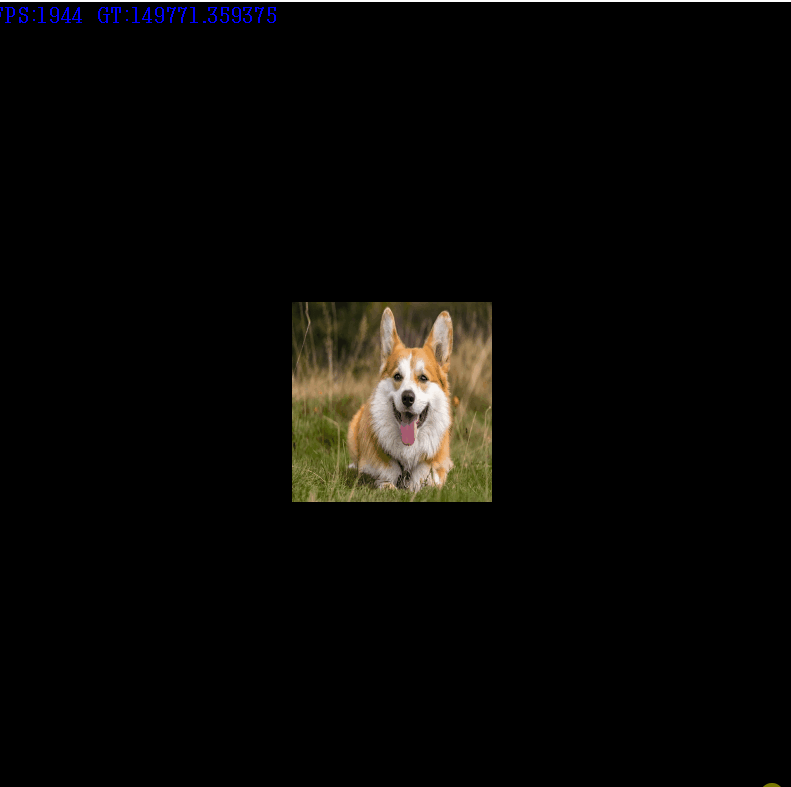
Translation행렬

Translation 행렬은 월드 공간에 올라갈 물체를 이동시킨다.

행렬의 _41,_42,_43값이 이동값에 해당되며 각각 x,y,z좌표를 나타낸다.

여기서 행렬을 4x4크기로 사용하는 이유가 이것인데, Scale과 Rotation을 그대로 적용시키면서 이동값도 그대로 한번에 적용시키기 위해 4x4크기의 행렬을 사용한다.

 

이것도 간단하므로 바로 테스트해보면

Matrix3x3 T;

// 우상 이동
T._31 = 2; 
T._32 = 2;


Vector2 v0 = m_rectObj->m_vertexList[0].vertexCoord;
Vector2 v1 = m_rectObj->m_vertexList[1].vertexCoord;
Vector2 v2 = m_rectObj->m_vertexList[2].vertexCoord;
Vector2 v3 = m_rectObj->m_vertexList[3].vertexCoord;

// w성분 추가. NDC좌표에서 수정하는것이므로 1.0이 아닌 0.1
Vector3 v0T = { v0.x,v0.y,0.1f };
Vector3 v1T = { v1.x,v1.y,0.1f };
Vector3 v2T = { v2.x,v2.y,0.1f };
Vector3 v3T = { v3.x,v3.y,0.1f };
//이동행렬 곱셈
v0T = v0T * T;
v1T = v1T * T;
v2T = v2T * T;
v3T = v3T * T;

// NDC좌표로 변환된 각 정점의 좌표들
m_rectObj->m_vertexList[0].vertexCoord = { v0T.x,v0T.y };
m_rectObj->m_vertexList[1].vertexCoord = { v1T.x,v1T.y };
m_rectObj->m_vertexList[2].vertexCoord = { v2T.x,v2T.y };
m_rectObj->m_vertexList[3].vertexCoord = { v3T.x,v3T.y };

 

이제 한번에 SRT행렬을 곱해서 적용시켜보자.

 -> 행렬의 결합법칙

Matrix3x3 S,R,T;
S._11 = 1.25f;
S._22 = 1.25f;

R._11 = cos(DegreeToRadian(10));
R._12 = sin(DegreeToRadian(10));
R._21 = -sin(DegreeToRadian(10));
R._22 = cos(DegreeToRadian(10));

T._31 = 1.0f;
T._32 = 0.0f;

Matrix3x3 SRT = S * R * T;


Vector2 v0 = m_rectObj->m_vertexList[0].vertexCoord;
Vector2 v1 = m_rectObj->m_vertexList[1].vertexCoord;
Vector2 v2 = m_rectObj->m_vertexList[2].vertexCoord;
Vector2 v3 = m_rectObj->m_vertexList[3].vertexCoord;

// w성분 추가. NDC좌표에서 수정하는것이므로 1.0이 아닌 0.1
Vector3 v0T = { v0.x,v0.y,0.1f };
Vector3 v1T = { v1.x,v1.y,0.1f };
Vector3 v2T = { v2.x,v2.y,0.1f };
Vector3 v3T = { v3.x,v3.y,0.1f };
//이동행렬 곱셈
v0T = v0T * SRT;
v1T = v1T * SRT;
v2T = v2T * SRT;
v3T = v3T * SRT;

// NDC좌표로 변환된 각 정점의 좌표들
m_rectObj->m_vertexList[0].vertexCoord = { v0T.x,v0T.y };
m_rectObj->m_vertexList[1].vertexCoord = { v1T.x,v1T.y };
m_rectObj->m_vertexList[2].vertexCoord = { v2T.x,v2T.y };
m_rectObj->m_vertexList[3].vertexCoord = { v3T.x,v3T.y };

이렇게 SRT변환은 컴퓨터 그래픽스에서의 변환과정 중에서 최종적으로 2D 스크린에 뿌려지기전에 로컬 -> 월드공간으로 변환하는 과정 . 앞으로 남은것은 뷰 좌표계, 투영 좌표계 이후 최종 스크린 좌표계까지의 단계가 남았다.

 -> 뷰 행렬 투영 행령 뷰포트 행렬.