bdfgdfg
정점 변환 - DirectX 렌더링 파이프라인 본문
정점 변환
컴퓨터 그래픽스에서 설명하는 렌더링 파이프라인은
로컬 -> 월드 -> 뷰 -> 투영 -> 최종 스크린의 변환의 단계를 의미한다.
로컬 공간은 로켈 좌표계에 있는 오브젝트가 존재하는 공간을 의미하며 모델 스페이스라고도 한다.

이렇게 물체중심의 좌표계를 우리의 게임 세상(월드 공간)에 올리기 위해 하나의 월드 공간의 원점을 기준으로 오브젝트를 배치한다.

게임 세상(월드 공간)에 올라가기전에 물체를 우리가 원하는 크기(Scale),회전(Rotation),이동(Translation)하여 월드 공간에 배치하기 위해 보통 월드 행렬이라는 Scale,Rotation,Translation행렬을 결합하여 각 정점을 곱연산하여 배치하게 된다.
-> 단위행렬이어도 상관없다.
-> 행렬의 결합법칙을 이용하여 정점의 S R T연산을 한번에 곱연산을 하여 연산량을 줄이는게 중요.
-> 각 물체는 월드 공간의 자신만의 월드 행렬을 하나씩 가지고 있다.
로컬 좌표와 월드 좌표의 개념이 헷갈릴 수 있지만 단순하게 로컬 좌표는 물체의 중심을 원점으로 하는 좌표.
월드 좌표는 월드 공간의 원점으로 물체를 배치하기 위한 좌표.

뷰 공간 (View Space, 카메라 공간이라고도 한다)은 게임 세상(월드 공간)에서 사용자가 카메라를 통해 볼 수 있는 영역을 의미한다.
-> 렌더링 되는 영역 카메라가 볼 수 없는곳은 렌더링 되지 않는다.(연산x)
-> 카메라를 왼쪽으로 이동하기 위해서 월드의 모든 정점을 오른쪽으로 이동시켜야 한다.★
뷰 변환은 카메라를 원점으로 하는 좌표계를 사용하여 월드에 있는 각 정점들을 카메라의 행렬을 만들어 변환시킨다.
그렇기에 카메라의 원점의 기저벡터를 구하는게 뷰변환의 첫번째 단계이다.
-> 월드 공간의 원점에서 카메라 공간의 카메라 좌표계에 맞추는 것.

우선 카메라의 위치를 Eye라 하고, 바라보는 위치를 Look이라고 할 때, 이 두 지점 사이의 벡터를 구하여 정규화를 하면 그 카메라의 z축을 구할 수 있게 된다.
예로들어 카메라의 위치가 0,10,-10 이고 바라보는 지점이 0,0,0이라 할 때
look - eye의 벡터의 뺄셈을 통해 나온 벡터를 정규화(Normalize)한다면 look을 바라보는 z축의 기저벡터가 만들어진다.
여기서 다음 카메라의 y와 x에 대한 기저벡터르 구해야하는데, DX에서 뷰 행렬을 구하는 함수를 살펴보면
D3DXMATRIX* D3DXMatrixLookAtLH(
_Inout_ D3DXMATRIX *pOut,
_In_ const D3DXVECTOR3 *pEye,
_In_ const D3DXVECTOR3 *pAt,
_In_ const D3DXVECTOR3 *pUp
);두번쨰 인자로 카메라의 위치, 세번쨰 인자로 바라보는 지점, 마지막인자로 Up벡터를 넘긴다.
이 Up벡터를 넘기는 이유는 보통의 상황에서는 y축의 기저벡터인 0,1,0과 z축은 직교할 가능성이 낮기에 임시로 건넨
(0,1,0)이라는 벡터를 y축으로 삼아 외적을 하여 x축 기저벡터를 구한다.
위와 같이 임시 y축 벡터를 통해 z축과 직교하는 x축 벡터를 만들었다면,
//의사코드
Vector3 upVector(0,1,0);
Vector3 zAxis = (Look - eye).Normalize; // z축 기저벡터를 구함
Vector3 xAxis = Cross(upVector,zAxis).Normalize();
Vector3 yAxis = Cross(zAxis,xAxis).Normalize(); // 정상적인 y축 기저벡터다시 z축과 x축을 외적하여 정상적인 y축 기저벡터를 구해야한다.
이제 카메라의 기저벡터를 구했으니 카메라를 원점으로 하여 각 물체들의 정점에 대한 변환이 이루어져야 한다.
즉 카메라가 월드에서 이동,회전 된다는 것은 월드 정점이 반대로 이동, 회전 되는 것이기 때문에 뷰행렬은 다음과 같게 된다.
- 카메라 좌표계를 기준으로 정점들을 변환시키기 위해서는 월드 좌표의 변환의 역과정을 밟으면 되는데 월드가 회전 -> 이동이었으니 카메라는 이동 -> 회전의 순으로 변환이다.
- 따라서, 카메라의 월드 좌표 변환 행렬의 역행렬이 곧 카메라 변환 행렬이다.
뷰(카메라) 행렬 = 카메라 이동 행렬(VT) * 카메라 회전 행렬(VR)
= 월드 이동행렬^-1 * 월드 회전행렬^-1 (^-1은 역행렬을 의미)
즉 위의 뷰 행렬을 3D 물체가 가지고 있는 월드 행렬에 곱해주는 것.
-> 카메라가 오른쪽으로 이동한다. 그렇다는 것은 3D물체는 그만큼 왼쪽으로 이동한다.
-> 그렇기 때문에 3D 물체의 행렬에 카메라의 월드 이동 행렬의 역행렬을 곱해주는 것.
-> 즉 월드 공간에 있는 3D 물체의 좌표를 카메라의 좌표에 맞춰 이동시키고 회전시키는 것
카메라의 이동행렬의 역행렬은 계산할 필요도 없다.

카메라의 이동좌표에 음수기호를 붙여 곱연산을 해보면 단위행렬이 나온다.

또한 카메라의 회전 행렬은 카메라의 기저벡터(x,y,z)를 담는 직교행렬.
-> 회전행렬은 특정 위치 기준을 돌리는 게 아닌 기저 벡터, 좌표계를 돌리는 것. (우리는 앞에서 카메라의 좌표계,기저벡터를 구했다)
--> 더 자세한 내용은 https://o-tantk.github.io/posts/derive-rotation-matrix/
직교행렬의 역행렬은 직교행렬의 전치행렬이라는 성질이 존재하기에 오른쪽과 같은 행렬로 나타낼 수 있다.
그렇기에 위의 두 행렬을 결합하면

위와 같은 뷰행렬이 만들어지는 것.
-> 마지막행은 행렬의 행과 열의 곱 즉 벡터의 성분끼리 곱하고 더하는 것이므로 내적으로 표시.
코드로 표현하면 밑과 같다.
Matrix4x4 ViewLookAt(Vector3& eye, Vector3& target, Vector3& up)
{
// ^연산자 오버로딩. (외적)
Matrix4x4 retViewMatrix;
Vector3 direction = (target - eye).Normal(); // Z Axis
Vector3 rightVector = (up ^ direction).Normal(); // X Axis
Vector3 upVector = (direction ^ rightVector).Normal(); // Y Axis (다시 y축 기저벡터 구하기)
//카메라의 기저벡터 구함.
matrix._11 = rightVector.x; matrix._12 = rightVector.x; matrix._13 = rightVector.x;
matrix._21 = rightVector.y; matrix._22 = rightVector.y; matrix._23 = rightVector.y;
matrix._31 = rightVector.z; matrix._32 = rightVector.z; matrix._33 = rightVector.z;
matrix._41 = -(eye.x * matrix._11 + eye.y * matrix._21 + eye.z * matrix._31);
matrix._42 = -(eye.x * matrix._12 + eye.y * matrix._22 + eye.z * matrix._32);
matrix._43 = -(eye.x * matrix._13 + eye.y * matrix._23 + eye.z * matrix._33);
return retViewMatrix;
}
이제 투영변환이다.
투영변환은 앞의 변환들 보다 난이도가 조금 높은 변환이다.
투영 변환의 개념
- 원근 투영으로 가까운 물체와 먼 거리의 물체를 크게 또는 작게 표현하여 원근감이 있게 하는 변환.
즉 게임세상에서 물체들이 원근감있게 보여질려면 정점들의 좌표를 투영변환을 통해 바꾸어야 한다는 의미.

원근감을 표현하기위해 위 그림과 같이 사각뿔의 앞부분이 잘린 시야영역을 사용한다.
그 절두체를 x축방향에서 보면 밑과 같은 그림이 나오는데

그 중 근평면이 우리의 모니터화면이고 카메라의 위치부터 근평면까지의 거리를 초점거리(d)라 한다.
시야각은 카메라에 설정가능한 FOV값이며 θ(세타)값을 알 수 있고, 모니터 화면(근평면) 높이의 절반값을 알 수 있다면 삼각함수를 이용하여 초점거리를 구할 수 있다.

모니터 화면의 해상도는 사용자마다 다르기에 정규화된 좌표계인 NDC를 이용하여 계산한다.
-> NDC는 중앙이 원점이며 가로,세로의 크기가 2인 좌표시스템

이제 각도와 높이를 알 수 있으니 초점거리를 구할 수 있다.

이제 절두체안에 있는 어떤 정점의 투영된 위치를 구해야한다.

위와 같이 절두체안에 존재하는 한 정점을 Pview라고 하고 근평면에 투영된 정점의 좌표를 Pndc라고 하고,
-> 정점 Pview는 이름에서 알 수 있듯이 뷰행렬 연산을 마치고 난 후의 정점.
초점에서 근평면의 Pndc에서 삼각형의 높이를 Yndc, 그리고 Pview가 있는 삼각형까지의 밑변을 Zview 높이를 Yview라고 한다면 밑과 같이 나타낼 수 있다.

위에서 각은 2분의 세타각을 이루는 닮은 꼴 삼각형이기에 비례식을 이용하여 밑과 같이 표현할 수 있다.

비례식을 풀어서 Yndc를 구하면

위와 같이 구할 수 있다.
이제 Xndc값을 구해야하는데 여기서 고려해야할 한가지가 더 있다. 바로 화면의 가로,세로 비율(aspect,종횡비)
모니터화면은 정사각형이 아닌 대부분 직사각형의 형태이므로 가로와 세로의 비율이 1:1로 대응되지 않는다.
-> DirectX로 친다면 윈도우의 클라이언트 영역 화면의 가로 세로 비율.
-> Xndc만을 aspect (가로 / 세로)로 나누는 이유는 가로영역이 늘어남에 따라 가로길이가 늘어남을 방지하기 위함.


종횡비를 고려하지 않은 경우.
-> 위는 DX환경에서 투영계산을 하지않고 NDC공간에서의 정점으로 바로 작성한 것.
-> NDC공간은 1:1 종횡비를 가짐.
그렇기에 Xndc를 구하기 위해서는 위와 같은 이유로 화면의 종횡비를 고려하여 구해야 한다.

위의 비례식을 풀어 Xndc를 구하면

위와같이 Xndc를 구할 수 있다.
-> 쉽게 생각해서 Yndc와 구하는 방법은 같지만, 화면의 종횡비를 생각하여 aspect값을 한번 더 나누어 주었다고 보면 된다.
이렇게 x,y를 구하여 뷰 행렬에의해 변환된 정점의 좌표에 x,y를 곱하면 물체는 그려지지만 아직 남은 문제가 있다.
깊이 문제.
-> DX에서는 DepthStencilView를 이용 (0 ~ 1의 깊이값을 가짐)
-> 0 ~ 1 사이의 깊이값을 z에 넣어야 한다.
뷰행렬연산을 마친 정점에서 근평면(NDC)에 투영된 x,y의 값은 구했으므로 그대로 행렬에 대입한다.

현재 x,y는 Zview라는 공통된 분모를 가진다. 여기서 생각할 수 있는 중요한 키워드는 동차좌표계의 특징인
x,y,z성분을 w로 나눠주는 것.
-> 즉 Zview를 w'라고 생각해본다면 식은 다음으로 좁힐 수 있다.
-> 참고로 d는 tan θ/2인걸 잊지말아야 한다.

이렇게 4열의 값을 구할 수 있다. w'성분을 Zview로 나오게끔하기 위해서 3행의 4열에 1이라는 값을 두는 것.
이제 남은값은 z값이다. x,y의값이 변경된다고 z에 영향을 끼칠일은 없기에 아래와 같이 행렬의 두 값을 더 구할 수 있다.

그리고 계산을 위해 위 식의 결과에서 다시 Zview로 나누어 준다.

마지막으로 A와 B를 구하는일만이 남았다.
우리는 Zndc가 near(근평면)는 0, far(원평면)는 1이라는 값이라는것을 알고있다.
그것을 통해 방정식을 세워보면

위와 같이 B값을 구할수있고 반대로 원평면이 1이므로 그에 대한 방정식도 세워보면
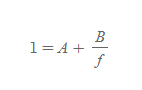
위와같이 구할 수 있다.
여기에서 위에서 구한 B값을 대입해보자.

B값을 대입하며 A값을 유도했고 이제 반대로 이렇게 구한 A도를 B = -An에 대입해보자. 그렇다면 B값도 유도가 가능하다.

이제 A와 B를 모두 구했으므로 최종 투영 변환 행렬이 구해졌다.

-> d가 1 / tan(θ/2)이라는 것.
이것을 코드로 표현해보면
Matrix PerspectiveFovLH(float near, float far, float fovy, float aspect)
{
float Yndc, Xndc, Zndc;
//fovy는 시야각
Yndc = 1 / tan(fovy * 0.5f); // 1 / tan(θ/2)
Xndc = Yndc / aspect; // 화면 종횡비 나누기.
Zndc = far / (far - near); // A를 구한 것.
Matrix ret;
::memset(&ret, 0, sizeof(Matrix));
ret._11 = Xndc;
ret._22 = Yndc;
ret._33 = Zndc;
ret._44 = -Zndc * near;
ret._34 = 1;
return ret;
}위에서 공식을 유도한대로 행렬을 채우는것을 알 수 있다.
이렇게 뷰변환이 된 정점에 위에서 구한 투영행렬을 곱하면 투영변환된 정점이 된다.
-> x,y는 -1 ~ 1사이의 값을. z는 0 ~ 1사이의 값을.
이 작업을 DX에서는 상수버퍼에 월드 행렬, 뷰 행렬, 투영 행렬을 넘겨 정점에다 곱하게 되는 것이고 그 과정은 DX11의 파이프라인중 정점 쉐이더에서 처리하게 된다.
cbuffer cbData
{
matrix g_matWorld : packoffset(c0);
matrix g_matView : packoffset(c4);
matrix g_matProj : packoffset(c8);
};
struct VS_OUT
{
float4 p : SV_POSITION;
float3 n : NORMAL;
float4 c : COLOR0;
float2 t : TEXCOORD0;
};
VS_OUT VS(float3 p: POSITION, float3 n : NORMAL,float4 c : COLOR, float2 t : TEXTURE)
{
VS_OUT output = (VS_OUT)0;
float4 local = float4(p,1.0f);
float4 world = mul( local, g_matWorld);
float4 view = mul( world, g_matView);
float4 proj = mul( view, g_matProj);
output.p = proj;
output.n = n;
output.c = c;
output.t = t;
return output;
}마지막으로 투영변환된 정점을 화면에다가 뿌릴 작업만이 남았다.
-> 마지막으로 정점에 뷰포트(렌더링할 사각 영역) 행렬을 곱해야 한다.
윈도우의 클라이언트 영역에 전체에다가 뿌리는 경우가 대부분이겠지만, 그렇지 않은 경우도 생각해야하기에 따로 뷰포트 행렬을 곱하는 과정도 존재하는 것.
어쨌든 NDC곤간의 좌표는 원점이 0,0이고 오른쪽으로 갈수록 X값이 +1 위로 갈수록 y값이 +1이 되는 좌표계.
이것을 우리가 보는 스크린화면에 맞추어 계산한다음 행렬을 만들어 곱해줘야 한다.

클라이언트 영역과 뷰포트 영역이 위와 같이 있을 때 변환된 좌표를 X,Y라고 할 때
X = Left
Y = Top
이렇게 시작한다.

현재 NDC공간에 있는 정점의 x값이 저 위치에 있다고 할 때,
X = Left + ((x + 1) / 2). -> ((x+1) / 2)는 비율.
여기서 뷰포트의 width값을 곱해주면 뷰포트에 올라갈 X좌표가 정해지는것. X = Left + ((x + 1) / 2) * width.
y의 경우 NDC공간에서 밑으로 갈수록 -이므로 1 - y.
즉 Y = Top + ((1 -y)/2) * Height인 것.
이것을 행렬로 다시 풀어써본다면

행렬에 들어갈 값들을 위에서 구한 X,Y를 통해 x,y성분을 넣어주고 상수부분을 넣어준다.
마지막으로 z값에 들어갈 부분을 MinDepth,MaxDepth를 정해줄 수 있다. (대부분 0.0,1.0으로 세팅)
그렇기에 최종 뷰포트 행렬의 결과는 밑과 같다.

그림이 너무 지저분하니 다른 사진으로 보면

위와 같다. X와 Y는 각각 LEFT,TOP.
DX11에서는 렌더링 파이프라인 중 레스터라이저단계에서 정점들의 뷰포트 매핑이 이루어진다.
BOOL DXDevice::SetViewport()
{
// 뷰포트 세팅
DXGI_SWAP_CHAIN_DESC getSwapDesc;
m_pSwapChain->GetDesc(OUT & getSwapDesc);
m_viewPort.TopLeftX = 0;
m_viewPort.TopLeftY = 0;
m_viewPort.Width = getSwapDesc.BufferDesc.Width;
m_viewPort.Height = getSwapDesc.BufferDesc.Height;
m_viewPort.MinDepth = 0.0f;
m_viewPort.MaxDepth = 1.0f;
m_pImmediateContext->RSSetViewports(1, &m_viewPort);
return TRUE;
}
보면 알겠지만, 우리가 뷰포트 행렬을 직접 만들어서 상수버퍼에 넘기거나 하는게 아니라 위와 같이 뷰포트를 설정해주면 알아서 파이프라인안에서 계산이된다.
참고 - https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=fear2002&logNo=221535494161
'게임프로그래밍 > DirectX11' 카테고리의 다른 글
| 변환(Transform) - Graphics (0) | 2022.03.15 |
|---|

